In this post I will introduce algorithm I use to lending USD on Bitfinex market.
Besides ordinary crypto-currency spot exchange Bitfinex also offers margin trading with BTC, LTC, ETH and USD. What does it mean? It means that you can borrow fiat or crypto from a liquidity provider(lender) at some interest rate and you can trade with that borrowed money and therefore effectively leverage your positions. If you want going short BTC/USD (sell BTC/USD) you simply borrow BTC and then sell them for USD. Conversely if you want going long BTC/USD(buy BTC/USD) you take an USD loan and buy BTC.
Some facts about the lending on Bitfinex
- The current lever is 3.3x – which means you can trade with 330% of your net balance so 330% = 100% of your own balance + 230% from a loan.
- The maintenance equity margin is 15% – that is when forementioned 100% net balance drops below 15% your positions get force liquidated.
- The expiration for loans is selected by the lender and is 2-30 days. Loan can be prematurely closed by borrower only.
- Bitfinex fee for providing liquidity lending feature is 15% of interest rate. Fee is deducted from lender’s earnings.
- Interest rate is paid once a 24 hours to the loan creditor(lender).
- The smallest time for which interest rate applies is 1 hour, any loan durable for less than 1 hour is considered as it lasted for 1 hour.
Particular loans are “traded” in very similar fashion as a BTC/USD on ordinary spot exchange. Just instead of price as primary order book driver we have an interest rate per day. Technically we call such an order book as FIFO continuous double auction and such a market as money market. Which orders get filled first? Clearly those orders with best interest rate hence the interest rate per day is the primary order book driver. What if there are more orders with same interest rate? We need a secondary order book driver which is in our case time of order arrival. This mechanism is called FIFO – first in first out from a queue of orders with same interest rate per day. We could easily use LILO (last in last out) instead of FIFO but it’s not a convention :). Continuous stands for the fact that order book is constantly updated and any of the lender or borrower can send order anytime. By this way the interest rate per day is “fully” driven by offer and demand of money market participants.
Let me quickly note that there exist “not FIFO continuous double auction” order books. How can they look like?
For example instead of FIFO matching algorithm we can have matching on pro-rata basis. Imagine that you have five orders with five volumes at one price level in an order book. Now arrives a market order with same price as is our price level but with not enough volume to sweep through all five limit orders. With FIFO matching this volume is matched only with orders with highest time priority(the earliest orders) but with pro-rata matching the given market order volume is matched with ALL of five limit orders and the market order volume is distributed proportionally with size of given five limit orders. This matching algorithm eliminates needs for “be first in queue” hence significantly reduces order cancellations and exchange servers load. On US stock markets ~96% of orders are cancelled so it does matter.
Instead of continuous there can be discrete matching of orders. We simply collect orders and match them say every hour. Non-matched orders are moved to a next matching. Discrete matching works as capacitor, it absorbs excessive volatility.
Lending bot design
I used basic statistics and few assumptions to design my bot. Let’s have a look into it.
Sample lending book:
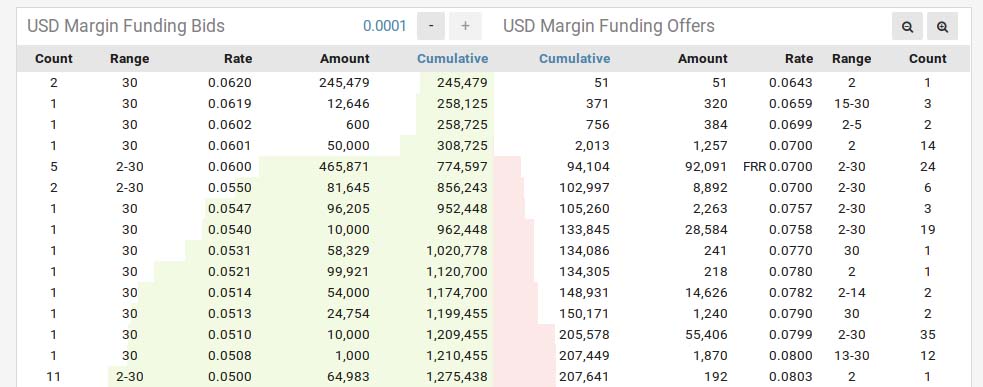
Central question is “Where to send my limit order?” Do I need to send it at the top of the offer side? Of course I don’t. Say I want the loan offer to be executed in 1 hour with at least 85% probabilty. That way I can slightly improve interest rate at which I lend my funds by a manner of eliminating loan offers at the lowest rates.
Volume threshold calculation
I can estimate interest rate of an order which is gonna to be executed with at least 85% probability in 1 hour by the following way.
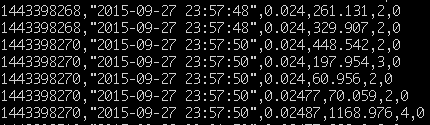
Download historical lending data from here. I’m using download script and cron because I want to have fresh .csv file for volume threshold calculation every day. If you are wondering what that mysterious “volume threshold” means, it’s a cumulative volume next to which is our desired interest rate with 85% probability of execution in 1 hour. It becomes more clear as we move ahead.
Example historical tick data .csv:
I compute the volume threshold based on last 10 days data. It should be enough to give some prediction power to the estimation. Let’s divide our tick data into 30 minute interval bins and sum corresponding volumes in particular intervals. In the following picture is the discrete PDF with 0.38 percentile.
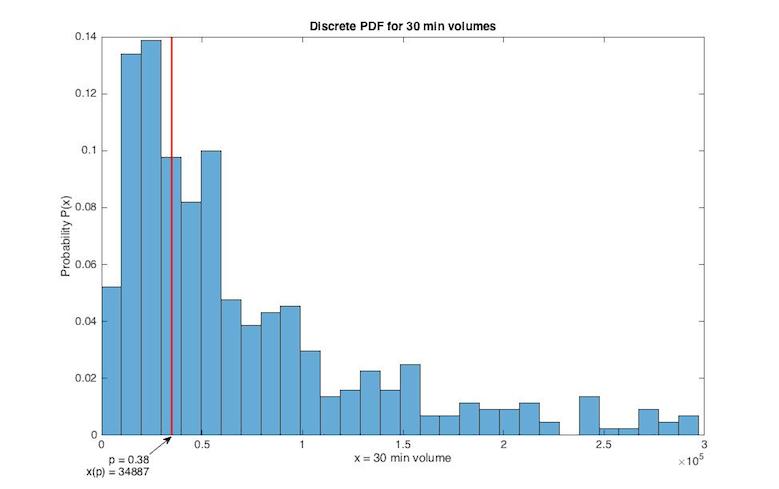
Let’s give some intuition behind the histogram. If I send a loan offer at cumulative volume level 34887 then there is the 62% probability of my order being executed in 30 minutes. In other words there is 62% probability that following 30 minute volume will be more than 34887 therefore our order will be executed. This probability holds for 30 min interval. What’s the probability of the order being executed in 1 hour … etc.? I use Bernoulli’s formula for binomial probability of getting at least k event in n trials:
![Rendered by QuickLaTeX.com \[ \sum \limit _{\tiny i=k}^{\tiny n}{n \choose i}p^i \times (1-p)^{n-i} = {2 \choose 1} \times 0.62^1 \times 0.38^1 + {2 \choose 2} \times 0.62^2 \times 0.38^0 = 0.8556 \]](https://mmquant.net/wp-content/ql-cache/quicklatex.com-e4a1cfb29cfbeb9875e18869b040120b_l3.png)
So if I send my loan offer at 34887 volume level (volume threshold) it should get executed in 1 hour with 85.6% probability. That’s it. See appendix for intuition behind the Bernoulli’s formula.
I run volume threshold calculation script once a day. Output from this script is naturally volume threshold which is in turn input for lending script itself.
Lending script
Before you use my lending script you need to download Bitfinex API MATLAB client. I will not go into details how to use this library because it’s quite straightforward. In a nutshell you need to generate key and corresponding secret (on BFX platform) and then insert both to the “key_secret” file. When you are finished, check “examples.m” file. I recommend you to read the short documentation along the library. It should take you just a few minutes.
So we have freshly calculated volume threshold, we have API client and keys/secrets in their place. Now we automate lending_script.m, threshold_calc.m and SizeCorrectionwget.sh by making an entry in crontab:
*/11 * * * * /usr/local/bin/matlab -nodesktop -nosplash -r lending_script > /dev/null 2>&1
5 0 * * * /usr/local/bin/matlab -nodesktop -nosplash -r threshold_calc > /dev/null 2>&1
55 23 * * * /home/maple/Documents/MATLAB/scripts/SizeCorrectionwget.sh
lending_script.m runs each 11 minutes, threshold_calc.m once a day at 00:05 and SizeCorrectionwget.sh once a day at 23:55. Note that there need to be set few custom paths in scripts. It’s completely up to you how you set them.
Logging
If you have waded through the lending_script.m code you have noticed a piece of logging code. It simply appends status line from last script execution to the selected log file. If you want your log files divided by week, month etc. then I recommend logrotate utility otherwise you will end up with just one long log file :).
Example log file:
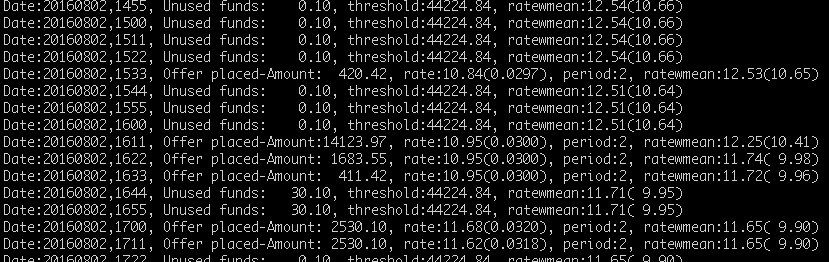
There are two types of entries in the log file. The first type – Unused funds … , is logged when there are no available funds to lend. Threshold is the volume threshold discussed above. Ratewmean is volume weighted average rate of all loans calculated by the following way:
![]() – volume of
– volume of ![]() loan
loan
![]() – price of
– price of ![]() loan
loan
![]() – volume weighted average rate
– volume weighted average rate
![]() – number of outstanding loans
– number of outstanding loans
![Rendered by QuickLaTeX.com \[ r_{vw}=\frac{\sum\limits_{\tiny i=1}^{\tiny n}p_i V_i}{\sum\limits_{\tiny i=1}^{\tiny n} V_i}. \]](https://mmquant.net/wp-content/ql-cache/quicklatex.com-f18b23a0e18fb83eefc8c7e4667862f8_l3.png)
Second value in brackets is ![]() so it’s net interest rate p.a. after fees deducted.
so it’s net interest rate p.a. after fees deducted.
Second type line is logged when there are funds available for lending. Amount is amount lent in dollars, rate is interest rate in % p.a.(%/100 per day) and period is set expiration time.
Results
Here is figure comparing my volume weighted portfolio rate and volume weighted BFX rate as a benchmark. The BFX rate is computed exactly as rvw above except that we take lending tick data and all prices with their respective volumes.
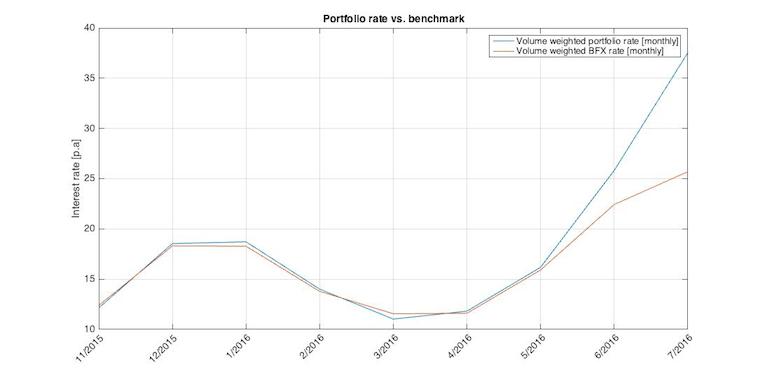
It can be clearly seen that at times with low BTC price volatility both rates are closely following each other. Volume threshold is very close to the best ask. Rates started diverge during May where BTC price became more volatile. Key role in rates divergence plays lending script feature which set different expirations for different rates. Currently it’s hardcoded into the script but I can imagine it could be optimized. Script sets 30 days expiration to loans with interest more than 20% p.a. (fees excluded).
Appendix: Bernoulli’s formula
Let’s translate the
![Rendered by QuickLaTeX.com \[ \sum \limit _{\tiny i=k}^{\tiny n}{n \choose i}p^i \times (1-p)^{n-i} = {2 \choose 1} \times 0.62^1 \times 0.38^1 + {2 \choose 2} \times 0.62^2 \times 0.38^0 = 0.8556 \]](https://mmquant.net/wp-content/ql-cache/quicklatex.com-e4a1cfb29cfbeb9875e18869b040120b_l3.png)
formula.
Let the ![]() is probability of success hence
is probability of success hence ![]() must be probability of failure (funds were lent vs. funds weren’t lent),
must be probability of failure (funds were lent vs. funds weren’t lent), ![]() is number of trials with at least
is number of trials with at least ![]() successes. Substitute “and” instead of
successes. Substitute “and” instead of ![]() and “or” instead of
and “or” instead of ![]() . Then we can write our event as
. Then we can write our event as
“probability of at least one success in two trials” = “probability of exactly one success in two trials” or “probability of exactly two successes in two trials”.
Exactly one success means that there will be exactly one success and one failure in two trials. We also have ![]() possibilities of doing such an event. Hence
possibilities of doing such an event. Hence
“probability of exactly one success in two trials” ![]() .
.
Exactly two successes are clear. This event means success in 1st trial and success in 2nd trial. Note that we have just ![]() possibility of doing so. Hence
possibility of doing so. Hence
“probability of exactly two successes in two trials” ![]() .
.
That way we can derive formula for at least ![]() successes in
successes in ![]() trials
trials
![Rendered by QuickLaTeX.com \[ \sum \limit _{\tiny i=k}^{\tiny n}{n \choose i}p^i (1-p)^{n-i} . \]](https://mmquant.net/wp-content/ql-cache/quicklatex.com-95376d17c58f0c840cee69c5ece7b8b7_l3.png)